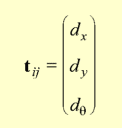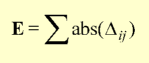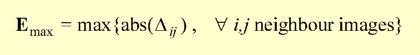|
Back to Home Page
Curriculum
Personal Achievements.
Research Interests
I am currently writing a PhD Thesis.
PC
Programs I wrote for my PC.
Spectrum
Published programs I wrote for my Spectrum
Electronics
Electronic Circuits I designed and built.
Personal Bookmarks
VRML Model of my face!
|
Research Interests
I am currently
writing a PhD Thesis at the
University of
Central Lancashire.
NEW! Have a look at the latest
results of my research here
My research
Abstract
Mosaic techniques have been used to obtain images with a large field
of view from video sequences by assembling individual overlapping images.
In existing methods of mosaic construction only consecutive frames are
aligned. Accumulation of small alignment errors occur, and in the case
of the image path returning to a previous position in the mosaic (looping
path), a significant mismatch between non-consecutive frames will result.
A new method for ensuring the consistency of the positions of all images
in a mosaic is described.
Motivation
My PhD project is concerned with graphic modelling techniques for virtual
reality applications. The increasing realism of computer generated graphics
in Virtual Reality applications such as special effects for films, video
games, virtual museums, etc. requires a number of qualified professionals
to perform the laborious task of building the graphic environments.
This project aims to investigate the capabilities of video for scanning
and modelling of environments for Virtual Reality applications. When scanning
becomes an easy and inexpensive task available to the user there will be
a revolution similar to the invention of photography, in which painters
were no longer needed to represent the reality in a picture.
Using inexpensive video cameras to create mosaics
Video is a low resolution medium that compares poorly with computer
displays and scanned images. It also suffers from a limited field of view.
Large objects can not be captured in a single picture. Using wide
angle lenses introduces substantial distortion and mapping an entire scene
into the limited resolution of a video camera compromises the quality of
the image. Mosaicing from video images is a solution, offering wide
field of view and high resolution.
Mosaic problem: Looping path
The construction of panoramic mosaics from video begins with the alignment
of successive frames of a video sequence. The images can be integrated
in a single large picture as the camera pans from left to right.
|
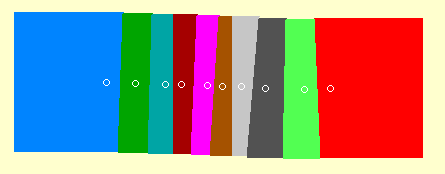
The colours represent different images. In this sequence the
camera never sweeps back. This type of panoramic mosaic can be easily composed
using commercially available software.
|
Although good alignment is achieved between successive images, cumulative
errors cause poor alignment when the image path follows a loop, i.e. when
the same area of the scene is covered by images which are distant in the
sequence.

|
Sequence showing a looping path. This type of mosaic cannot
be composed correctly by any commercial software.
|
The effects of the looping path problem are dramatic
when large numbers of images are involved in the loop. In addition, the
misalignment is unavoidable even when the frame-to-frame displacement has
been computed very accurately.
Click on image to view full size mosaic. (592 Kb)

|
Note the misplacement of the images at the intersection of the
path.
|
Solution to Looping Path Problem
For the rigid model, a translation (dx, dy)
and a rotation angle dq
of image j with respect to image i, correctly describe their
relative position.
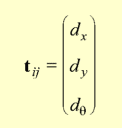
The relative position of a neighbour pair of images will be modified
slightly without introducing a visible loss in quality. Such a change from
the computed position must not exceed a fraction of a pixel if the seam
is to remain unnoticeable.
The solution uses an analogy with a physical model, consisting of a
network of connected nodes representing the centres of the images on which
forces are exerted in order to change their position. The links between
nodes are defined by the transformations that align neighbour images. In
this analogy f (Dij) represents the force
pushing image i towards the right position with respect to image
j, where the function f models the force.
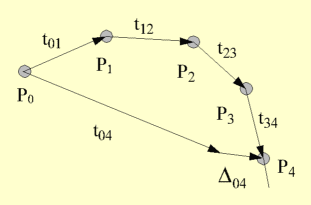
| Relation between the positions of the images in the mosaic P0,
P1, P2, P3, P4 and the relative
positions t01, t12, t23, t34
that align successive images. D04
is the error between the computed relative position of images 0 and
4 ( t04 ) and their actual relative
position in the mosaic (P4 - P0). The circles
represent the centres of the images. |
The performance of the function f (Dij)
is assessed by inspection of the overall distortion E and the error
for the worst case Emax once equilibrium is achieved.
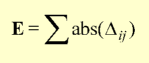 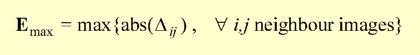
| Process
Calc_Successive_Image_Alignments();
Set_Initial_Positions();
DO {
DO {
Calc_Forces();
Modify_Positions();
} UNTIL (stability is achieved);
Calc_New_Neighbours();
} UNTIL (no new neighbours arise);
Render_Mosaic(); |
At the end of the process the cumulative error is spread across all
images, and therefore no single pair of images shows a marked misalignment.
Results
The technique for solving the looping path problem has been tested
with various sets of images resulting in excellent overall improvement
of the mosaic.
Document Mosaic
The images of the Document Mosaic shown here were taken with a video
camera fixed over a desk and sliding the document:

|
1663x2320 pixels mosaic, composed of 141 images (736x560 pixels).
The colours represent the areas used from different images. The path followed
by the camera is superimposed.
|
Click on this image to view full size mosaic. (243
Kb)

|
Alignment on consecutive frames only showing misalignment
due to looping path problem.
|
Click on this image to view full size mosaic. (241
Kb)

|
Alignment after error distribution showing images in correct
positions.
|
| Document Mosaic |
Emax
|
Between Images
|
Sum Error E
|
Average Error per seam
|
| x (pixels) |
0.6823
|
128 and 118
|
63.11
|
0.1783
|
| y (pixels) |
0.5386
|
105 and 57
|
75.63
|
0.2136
|
| q (rads) |
0.002597
|
7 and 6
|
0.3728
|
0.001053
|
Table 1: Document Mosaic, 141 images, 354 pairs of neighbour images.
The table shows the errors present after readjustment. In the worst case
the images have been displaced by about half a pixel from their computed
position.
Another example: Lab Mosaic
The images for the mosaic named ‘Lab’ were obtained with a hand held
video camera from a fixed location, and despite the parallax and the distortion
from mapping of a spherical view on a flat image, the results are promising:
Click on this image to view full size mosaic. (464
Kb)

|
The 130 images in this mosaic were obtained with a hand held
video camera from a fixed location. Note the improvement with respect to
the alignment on consecutive images only, shown above.
|
| Mosaic "Lab" |
Emax
|
Between Images
|
Sum Error E
|
Average Error per seam
|
| x (pixels) |
0.9934
|
123 and 62
|
71.64
|
0.2372
|
| y (pixels) |
1.0576
|
82 and 81
|
77.65
|
0.2571
|
| q (rads) |
0.01610
|
123 and 65
|
1.186
|
0.003927
|
Table 2: Mosaic ‘Lab’, 130 images, 302 pairs of neighbour images. The
errors are higher than in the other mosaics due to errors in the computation
of image alignment caused by parallax. In addition, the field of view is
about 90°, so further distortions are introduced by the mapping onto
a plane.
Conclusions
It has been shown that a new step must be introduced in video mosaic
construction to account for the looping path problem. Cumulative errors
occur in successive image alignment, and in the case of the image path
returning to a previous position in the mosaic, a significant mismatch
between non-successive images will result. The proposed solution makes
use of the alignments between all neighbour images to consistently position
the images on the mosaic. Starting with the successive image alignment
positions, these are modified by small increments to reduce the overall
misalignment error.
Further work: Spherical mosaic
Since the field of view is not a limitation when using this approach,
360° mosaics can now be produced. Current research aims at full spherical
mosaics for applications in Virtual Reality.
Considering the projective transformation matrix as a representation
of the position and orientation of a camera in space, an analogous method
using forces can be used for the consistent alignment of all images in
the mosaic using the projective model.
References
M. Guillén González, Phil Holifield, Martin Varley, "Improved
Mosaic Construction by Accumulated Alignment Error Distribution", Proceeding
of the British Machine Vision Conference 1998, Vol. 2, pp.377-387. ISBN
1-901725-04-9
Paul R. Wolf, "Elements of photogrammetry (with air photo interpretation
and remote sensing)". - New York; London : McGraw-Hill, 1974.
R. Szeliski, "Video Mosaics for Virtual Environments", IEEE Workshop
on Applications of Computer Vision, pp. 44-53, 1994.
S. Mann and R. W. Picard, "Virtual Bellows: constructing high quality
stills from video", IEEE International Conference on Image Procesing, pp.
363-367, 1994.
H. S. Sawhney, R. Kumar, "True Multi-Image Alignment And Its Application
To Mosaicing And Lens Distortion Correction", Proceedings of the IEEE Computer
Society Conference on Computer Vision and Pattern Recognition, pp. 450-456,
1997.
P. J. Burt, M. Hansen, P. Anandan, "Video Mosaic Displays", Proceedings
of SPIE - International Society for Optical Engineering, Vol. 2736, pp.119-127,
1996.
R. Szeliski, "Image Mosaicing for Tele-Reality Applications", Cambridge
Research Laboratory, Technical Report Series, May 1994.
S. Peleg and J. Herman, "Panoramic mosaics by manifold projection",
IEEE Conference on Computer Vision and Pattern Recognition, pp. 338-343,
San Juan, Puerto Rico, June 1997.
Rik D. T. Janssen and A. M. Vossepoel, "Compilation Of Mosaics From
Separately Scanned Line Drawings", IEEE Workshop on Applications of Computer
Vision - Proceedings, pp. 36-43, 1994.
A. Zappala, A. Gee, M. Taylor, "Document Mosaicing", Proceedings of
the British Machine Vision Conference, Vol. 2, pp. 600-609, 1997.
M. Hansen, P. Anandan, K. Dana, G. van der Wal, P. Burt, "Real-time
Scene Stabilization and Mosaic Construction", IEEE Workshop on Applications
of Computer Vision - Proceedings, pp.54-62, 1994.
F. Aurenhammer, "Voronoi diagrams: A survey of a fundamental geometric
data structure", ACM Comp. Surv., 23:345-405, 1991.
M. Irani, P. Anandan, S. Hsu, "Mosaic Based Representations of Video
Sequences and Their Applications", IEEE International Conference on Computer
Vision, pp. 605-611, 1995.
|
|